Programas de ejemplo en Prolog

01 Mínimo común múltiplo
02 Máximo común divisor
03 Factorial
04 Potenciación
05 Sumatorias
06 Producto
07 Programa de parentesco sin menú
08 Programa de parentesco con menú
09 Arboles binarios
10 Operaciones con listas
11 Sucesión de números naturales
12 Problema de las 8 reinas

MCM

El siguiente programa calcula el mínimo común multiplo de dos números, para ello los datos se deben ingresar de la siguiente manera: mcm(A, B, A1, B1, C). A y B son los dos números a ingresar, A1 y B1 toman el mismo valor de A, B y C se ingresa sin ningún valor. Quedaria así: mcd(12, 20, 12, 20, C) obteniendo como resultado 60.



domains

A,B,C,A1,B1=integer

predicates

mcm(A,B,A1,B1,C)

clauses

mcm(A,B,A1,B1,C):-A=B,C=A*(A1/A)*(B1/A).
mcm(A,B,A1,B1,C):-A>B,X=A-B,mcm(X,B,A1,B1,C).
mcm(A,B,A1,B1,C):-A
Regresar al indice

MCD

El siguiente programa calcula el máximo común divisor de dos números, para ello los datos se deben ingresar de la siguiente manera: mcd(A, B, C). A y B son los dos números a ingresar y C se ingresa sin ningún valor. Quedaria así: mcd(48, 60, C) obteniendo como resultado 12.



domains

A, B, C = integer

predicates

mcd(A, B, C)

clauses

mcd(A,B,C):-A = B,C = A.
mcd(A,B,C):-A > B, X = A - B, mcd(X, B, C).
mcd(A,B,C):-A < B, Y = B - A, mcd(A, Y, C).

Regresar al indice

FACTORIAL

El siguiente programa calcula el factorial de un número N. El ejemplo es: FACTO(1,1,N) se deben poner siempre los 2 primeros unos y calcula el factorial.

DOMAINS

NUM = INTEGER

PREDICATES

FACTO(NUM,NUM,NUM)

CLAUSES

FACTO(A,B,C):-X=B+1,Z=A*X,X<=C,
WRITE(Z),NL,FACTO(Z,X,C).

Regresar al indice

POTENCIACIÓN

El siguiente programa calcula la potencia de un numero, para ello se deben ingresar los datos de la siguiente forma: exponente(A, B, C, D). A es el número base y B es el exponente, en C coloca un 1 y D toma el mismo valor de A. Quedaria asi: exponente(3,2,1,3) para obtener como resultado 9.

domains

var = real

predicates

exponente(var, var, var, var)

clauses

exponente(A, B, C, D):- Y = C+1, N = A * D, C < B, write("EXP = ", D, "*", A, "=", N), nl, exponente(A, B, Y, N)

Regresar al indice

SUMATORIAS

El siguiente programa calcula la sumatoria de los N primeros numeros enteros positivos, para ello los datos se deben ingresar de la siguiente forma: suma(A,B,C). A toma el valor de 1, B toma el valor de 1 y en C toma el valor de los N numeros a sumar. Quedaria así: suma(1,1,3) obteniendo la sumatoria desde 1 hasta 3 igual 6.

domains

var = real

predicates

suma(var, var, var)

clauses

suma(A,B,C):- X = B + 1, Z= A + X, X <= C, write("SUM =",A ,"+", X, "=",Z), nl, suma(Z, X, C).

Regresar al indice

PRODUCTO

El siguiente programa calcula el producto de dos números utilizando sumas sucesivas, para ello los datos se deben ingresar de la siguiente forma: mult(A, B, C, D). A y B son los numero a multiplicar, en C coloca un 1 y D toma el mismo valor de A. Quedaria así: mult(3, 5, 1, 3) obteniendo como resultado 15.

domains

var = real

predicates

mult(var, var, var, var)

clauses

mult(A,B,C,D):- Z = C + 1, L=A + D, C < B, write("MULTIPLICACION = ",D," + ",A," = ", L), nl, mult(A,B,Z,L).

Regresar al indice

PARENTESCO 1

El siguiente programa esta hecho en lenguaje de programacion lógica Prolog y su función es la de calcular cualquier parentesco en el árbol genaológico de una familia, como por ejemplo los hijos son de tal padre, el abuelo tiene los siguientes nietos, los hermanos son y así sucesivamente.


domains

perso=symbol

predicates

hombre(perso)
mujer(perso)
pariente(perso,perso)
padre(perso,perso)
madre(perso,perso)
hijo(perso,perso)
hija(perso,perso)
hermano_de(perso,perso)
hermana_de(perso,perso)
abuelo(perso,perso)
abuela(perso,perso)
tio_de(perso,perso)
ancestro(perso,perso,perso)

clauses

hombre(francisco).
hombre(juan).
hombre(benito).
hombre(arcecio).
hombre(alex).
mujer(caterine).
mujer(isabel).
mujer(julia).
mujer(ana).
mujer(cristina).
mujer(laura).
mujer(silvia).
pariente(francisco,juan).
pariente(francisco,julia).
pariente(francisco,ana).
pariente(caterine,juan).
pariente(caterine,julia).
pariente(caterine,ana).
pariente(juan,arcecio).
pariente(juan,cristina).
pariente(isabel,arcecio).
pariente(isabel,cristina).
pariente(ana,alex).
pariente(ana,laura).
pariente(ana,silvia).
pariente(benito,alex).
pariente(benito,laura).
pariente(benito,silvia).
padre(X,Y):-hombre(X),pariente(X,Y).
madre(M,N):-mujer(M),pariente(M,N).
hijo(H,K):-hombre(H),pariente(K,H).
hija(L,M):-mujer(L),pariente(M,L).
hermano_de(H,O):-hombre(H),padre(L,H),padre(L,O),H<>O.
hermana_de(H,A):-mujer(H),madre(X,H),madre(X,A),H<>A.
abuelo(X,L):-hombre(X),padre(X,Y),pariente(Y,L).
abuela(Y,L):-mujer(Y),madre(Y,K),pariente(K,L).
tio_de(T,S):-hombre(T),hermano_de(T,P),madre(P,S) or hombre(T),hermano(T,P),padre(P,S).
ancestro(A,P,L):-pariente(A,P),pariente(P,L).

Regresar al indice

PARENTESCO 2

El siguiente programa esta hecho en lenguaje de programación lógica Prolog y su función es la de calcular cualquier parentesco en el árbol genaológico de una familia utilizando un menú que le permite escoger que parentescos quiere hayar, como por ejemplo los hijos son de tal padre, el abuelo tiene los siguientes nietos, los hermanos son y así sucesivamente.



domains

repla = symbol
perso=symbol

predicates

hombre(perso)
mujer(perso)
pariente(perso,perso)
padre(perso,perso)
madre(perso,perso)
hijo(perso,perso)
hija(perso,perso)
hermano(perso,perso)
hermana(perso,perso)
tio(perso,perso)
tia(perso,perso)
abuelo(perso,perso)
abuela(perso,perso)
ancestro(perso,perso)

run
case(string)

goal
run .

clauses

hombre(francisco).
hombre(juan).
hombre(benito).
hombre(arcecio).
hombre(alex).
mujer(caterine).
mujer(isabel).
mujer(julia).
mujer(ana).
mujer(laura).
mujer(silvia).
mujer(cristina).
pariente(francisco,juan).
pariente(francisco,isabel).
pariente(francisco,ana).
pariente(caterine,juan).
pariente(caterine,isabel).
pariente(caterine,ana).
pariente(juan,arcecio).
pariente(juan,cristina).
pariente(isabel,arcesio).
pariente(isabel,cristina).
pariente(ana,alex).
pariente(ana,laura).
pariente(ana,silvia).
pariente(benito,alex).
pariente(benito,laura).
pariente(benito,silvia).

run :- clearwindow, makewindow(2,3,14," UNIVERSIDAD SANTIAGO DE CALI ",2,2,20,70),
write('\n','\n'),
write(" _____ MENU ______",'\n','\n'),
write(" Padre ..................... : P ",'\n'),
write(" Madre ..................... : M ",'\n'),
write(" Hermano ..................... : H ",'\n'),
write(" Hermana ..................... : K ",'\n'),
write(" Tio ..................... : T ",'\n'),
write(" Tia ..................... : W ",'\n'),
write(" Abuelo ..................... : A ",'\n'),
write(" Abuela ..................... : G ",'\n'),
write(" Salir ..................... : S ",'\n','\n'),
write(" Cual es su eleccion ............. : "),
readln(N),
write('\n'),
upper_lower(E,N),
case(E),
"E" = "Q".
run if run.

/***** REGLAS ******/

padre(X,Y):-hombre(X),pariente(X,Y).
madre(M,Y):-mujer(M),pariente(M,Y).
hijo(Y,X):-hombre(X),padre(Y,X).
hija(Y,X) :- mujer(Y),pariente(X,Y).
hermano(Y,Z):-hombre(Y),padre(X,Z),padre(X,Y),Y<>Z.
hermana(Y,Z):-mujer(Y),madre(X,Y),madre(X,Z),Y<>Z.
tio(X,Y):-hombre(X),hermano(X,Z),madre(Z,Y) or hombre(X),hermano(X,Z),padre(Z,Y).
tia(X,Y):-mujer(X),hermana(X,Z),madre(Z,Y) or mujer(X),hermana(X,Z),padre(Z,Y).
abuelo(Z,Y):-hombre(Z),padre(Z,X),padre(X,Y) or hombre(Z),padre(Z,X),madre(X,Y).
abuela(Z,Y):-mujer(Z),madre(Z,X),padre(X,Y) or mujer(Z),madre(Z,X),madre(X,Y).
ancestro(X,Y):-hombre(X),padre(X,Y) or hombre(X),tio(X,Y) or hombre(X),abuelo(X,Y) or mujer(X),madre(X,Y) or mujer(X),tia(X,Y) or mujer(X),abuela(X,Y).

/****************************************************************************/
/********************* GOALS INTERNOS *************************/

case("P") :- clearwindow, padre(X,Y), write(" el padre es : ", X, " de " , Y),nl,
write(" ENTER ",'\174','\217', " para la siguiente solucion ......."),
nl,readln(_), fail,readln(_).

case("M") :- clearwindow, madre(M,Y), write(" la madre es: ", M , " de :" , Y),nl, write("ENTER ",'\174','\217',
" para la siguiente solucion ......."), readln(_), nl,fail.

case("T") :- clearwindow, tio(X,Y), write(" El tio es : " , X , " de " ,Y ),nl, write(" ENTER ",'\174','\217',
" para la siguiente solucion ......."), readln(_), nl,fail.

case("W") :- clearwindow, tia(X,Y), write(" La tia es : " , X , " de :" , Y),nl, write(" ENTER ",'\174','\217',
" para la siguiente solucion ......."), readln(_), nl,fail.

case("A") :- clearwindow, abuelo(Z,Y), write(" El abuelo es : " , Z , " de " , Y),nl, write("ENTER ",'\174','\217',
" para la siguiente solucion ......."), readln(_), nl,fail.

case("G") :- clearwindow, abuela(Z,Y), write(" La abuela es: ", Z , " de: " , Y),nl, write("ENTER ",'\174','\217',
" para la siguiente solucion ......."), readln(_), nl,fail.

case("H") :- clearwindow, hermano(Y,Z), write(" El hermano es :" ,Y, " de : " , Z),nl, write("ENTER ",'\174','\217',
" para la siguiente solucion ......."), readln(_), nl,fail.

case("K") :- clearwindow, hermana(Y,Z), write(" La hermana es :" , Y, " de : ", Z ),nl, write(" ENTER ",'\174','\217',
" para la siguiente solucion ......."), readln(_), nl,fail.

case("S") :- clearwindow, cursor(10,15), write(" FIN DEL PROGRAMA .............."),
exit, nl.


Regresar al indice

ARBOLES BINARIOS

/* ARBOLES BINARIOS */

arbol_binario(v).
arbol_binario(nodo(Raiz,Izq,Der)) :- arbol_binario(Izq),
arbol_binario(Der).

esta(X,nodo(X,Izq,Der)).
esta(X,nodo(Y,Izq,Der)) :- esta(X,Izq); esta(X,Der).

isomorfos(v,v).
isomorfos(nodo(X,I1,D1),nodo(X,I2,D2)) :- isomorfos(I1,I2),
isomorfos(D1,D2).

isomorfos(nodo(X,I1,D1),nodo(X,I2,D2)) :- isomorfos(I1,D2),
isomorfos(D1,I2).

sustituir(X,Y,v,v).
sustituir(X,Y,nodo(X,I1,D1),nodo(Y,I2,D2)) :- sustituir(X,Y,I1,I2),
sustituir(X,Y,D1,D2).
sustituir(X,Y,nodo(Z,I1,D1),nodo(Z,I2,D2)) :- X\=Z,
sustituir(X,Y,I1,I2),
sustituir(X,Y,D1,D2).


preorden(v,[]).
preorden(nodo(X,I,D),Xs) :- preorden(I,Ys), preorden(D,Zs),
concatena([X|Ys],Zs,Xs).

inorden(v,[]).
inorden(nodo(X,I,D),Xs) :- inorden(I,Ys), inorden(D,Zs),
concatena(Ys,[X|Zs],Xs).

postorden(v,[]).
postorden(nodo(X,I,D),Xs) :- postorden(I,Ys), postorden(D,Zs),
concatena(Ys,Ws,Xs),
concatena(Zs,[X],Ws).

concatena([],Ys,Ys).
concatena([X|Xs],Ys,[X|Zs]) :- concatena(Xs,Ys,Zs).

subarbol(X,X).
subarbol(Sub,nodo(Y,Izq,Der)) :- iguales(Sub,Izq);
iguales(Sub,Der);
subarbol(Sub,Izq);
subarbol(Sub,Der).
iguales(v,v).
iguales(nodo(X,I1,D1),nodo(X,I2,D2)) :- iguales(I1,I2), iguales(D1,D2).


insertar(X,v,arbol(X,v,v)).
insertar(X,arbol(Y,I,D),arbol(Y,I1,D)) :- X<Y, insertar(X,I,I1).
insertar(X,arbol(Y,I,D),arbol(Y,I,D1)) :- X>Y, insertar(X,D,D1).

eliminar(X,arbol(X,v,v),v).
eliminar(X,arbol(Y,I,D1),arbol(Y,I,D2)) :- X>Y, eliminar(X,D1,D2).
eliminar(X,arbol(Y,I1,D),arbol(Y,I2,D)) :- X<Y, eliminar(X,I1,I2).
eliminar(X,arbol(X,I,D1),arbol(Z,I,D2)) :- vacio(I),minimo(D1,Z),
eliminar(Z,D1,D2).
eliminar(X,arbol(X,I1,D),arbol(Z,I2,D)) :- maximo(I1,Z),
eliminar(Z,I1,I2).
minimo(arbol(X,v,_),X).
minimo(arbol(X,I,D),Y) :- minimo(I,Y).

maximo(arbol(X,_,v),X).
maximo(arbol(X,I,D),Y) :- maximo(D,Y).

vacio(v).

Regresar al indice

OPERACIONES CON LISTAS

/* OPERACIONES CON LISTAS */

lista([]).
lista([X|Xs]) :- lista(Xs).

pertenece(X,[X|Xs]).
pertenece(X,[Y|Ys]) :- pertenece(X,Ys).

prefijo([],Xs).
prefijo([X|Xs],[X|Ys]) :- prefijo(Xs,Ys).

prefijo2(Xs,Ys) :- concatena(Xs,Ws,Ys).

sufijo(Xs,Xs).
sufijo(Xs,[Y|Ys]) :- sufijo(Xs,Ys).

sufijo2(Xs,Ys) :- concatena(Ws,Ys,Xs).

sublista(Xs,Ys) :- prefijo(Ws,Ys), sufijo(Xs,Ws).

sublista2(Xs,Ys) :- prefijo(Xs,Ws), sufijo(Ws,Ys).

sublista3(Xs,Ys) :- prefijo(Xs,Ys).
sublista3(Xs,[Y|Ys]) :-sublista(Xs,Ys).

sublista4(Xs,AsXsBs) :- concatena(As,XsBs,AsXsBs), concatena(Xs,Bs,XsBs).

concatena([],Ys,Ys).
concatena([X|Xs],Ys,[X|Zs]) :- concatena(Xs,Ys,Zs).

pertenece2(X,Xs) :- sublista([X],Xs).

pertenece3(X,Ys) :- concatena(Ws,[X|Zs],Ys).

inversa([],[]).
inversa([X|Xs],Ys) :- inversa(Xs,Ws), concatena(Ws,[X],Ys).

inversa2(Xs,Ys) :- inversa2(Xs,[],Ys).
inversa2([X|Xs],Acc,Ys) :- inversa2(Xs,[X|Acc],Ys).
inversa2([],Ys,Ys).

adyacentes(X,Y,Zs) :- concatena(As,[X,Y|Bs],Zs).

longitud([],0).
longitud([X|Xs],N) :- longitud(Xs,M), N is M+1.

ultimo(Xs,Y) :- concatena(Ws,[Y],Xs).

borra([],X,[]).
borra([X|Xs],X,Ys) :- borra(Xs,X,Ys).
borra([X|Xs],Z,[X|Ys]) :- X\=Z, borra(Xs,Z,Ys).

borra_primer(X,[X|Xs],Xs).
borra_primer(X,[Y|Ys],[Y|Zs]) :- borra_primer(X,Ys,Zs).

ordenada([X]).
ordenada([X,Y|Ys]) :- X=<Y, ordenada([Y|Ys]).

permuta([],[]).
permuta(Xs,[Z|Zs]) :- borra_primer(Z,Xs,Ys), permuta(Ys,Zs).

inserta(X,Ys,Zs) :- borra_primer(X,Zs,Ys).

ordena(Xs,Ys) :- permuta(Xs,Ys), ordenada(Ys).

inserta2(X,[],[X]).
inserta2(X,[Y|Ys],[X,Y|Ys]) :- X=<Y.
inserta2(X,[Y|Ys],[Y|Zs]) :- X>Y, inserta2(X,Ys,Zs).

ordena2([],[]).
ordena2([X|Xs],Ys) :- ordena2(Xs,Zs), inserta2(X,Zs,Ys).

quicksort([],[]).
quicksort([X|Xs],Ys) :- partir(Xs,X,Menores,Mayores),
quicksort(Menores,Ax),
quicksort(Mayores,Bx),
concatena(Ax,[X|Bx],Ys).

partir([],_,[],[]).
partir([X|Xs],Y,[X|Menores],Mayores) :- X=<Y, partir(Xs,Y,Menores,Mayores).
partir([X|Xs],Y,Menores,[X|Mayores]) :- X>Y, partir(Xs,Y,Menores,Mayores).

sustituir(_,_,[],[]).
sustituir(X,Y,[X|Xs],[Y|Ys]) :- sustituir(X,Y,Xs,Ys).
sustituir(X,Y,[Z|Xs],[Z|Ys]) :- sustituir(X,Y,Xs,Ys).

no_repetir([],[]).
no_repetir([X|Xs],Ys) :- pertenece(X,Xs), no_repetir(Xs,Ys), !.
no_repetir([X|Xs],[X|Ys]) :- not(pertenece(X,Xs)), no_repetir(Xs,Ys).

mergesort([X],[X]) :- !.
mergesort([],[]).
mergesort(Xs,Ys) :- separa(Xs,Ws,Zs),
mergesort(Ws,Ws2),
mergesort(Zs,Zs2),
junta(Ws2,Zs2,Ys).


separa([],[],[]).
separa([X],[X],[]).
separa([X,Y|Ys],[X|Xs],[Y|Zs]) :- separa(Ys,Xs,Zs).

junta(Xs,[],Xs).
junta([],Xs,Xs).
junta([X|Xs],[Y|Ys],[X|Zs]) :- X<Y, junta(Xs,[Y|Ys],Zs).
junta([X|Xs],[Y|Ys],[Y|Zs]) :- X>=Y, junta([X|Xs],Ys,Zs).

Regresar al indice

SUCESIÓN DE NÚMEROS NATURALES

/*SUCESION DE NATURALES*/

nat(cero).
nat(suc(X)) :- nat(X).

menor_igual(cero,X) :- nat(X).
menor_igual(suc(X),suc(Y)) :- menor_igual(X,Y).

suma(X,cero,X) :- nat(X).
suma(X,suc(Y),suc(Z)) :- suma(X,Y,Z).

resta(X,Y,Z) :- suma(Y,Z,X).

producto(X,cero,cero) :- nat(X).
producto(X,suc(Y),Z) :- producto(X,Y,W), suma(W,X,Z).

potencia(cero,suc(X),cero) :- nat(X).
potencia(X,cero,suc(cero)) :- nat(X).
potencia(X,suc(Y),Z) :- potencia(X,Y,W), producto(W,X,Z).

factorial(cero,suc(cero)).
factorial(suc(X),Y) :- factorial(X,W), producto(W,suc(X),Y).

minimo(suc(X),cero,cero) :- nat(X).
minimo(cero,suc(Y),cero) :- nat(Y).
minimo(suc(X),suc(Y),suc(Z)) :- minimo(X,Y,Z).

minimo2(X,Y,X) :- menor_igual(X,Y).
minimo2(X,Y,Y) :- menor_igual(Y,X).

modulo(X,X,cero) :- nat(X).
modulo(X,Y,X) :- menor(X,Y).
modulo(X,Y,Z) :- mayor(X,Y), resta(X,Y,W), modulo(W,Y,Z).

cociente(X,Y,cero) :- nat(X), nat(Y), menor(X,Y).
cociente(X,Y,suc(Z)) :- resta(X,Y,W), cociente(W,Y,Z).

menor(cero,suc(X)) :- nat(X).
menor(suc(X),suc(Y)) :- menor(X,Y).

mayor(X,Y) :- not(menor_igual(X,Y)).

ackermann(cero,N,suc(N)) :- nat(N).
ackermann(suc(M),cero,N) :- ackermann(M,suc(cero),N).
ackermann(suc(M),suc(N),P) :- ackermann(suc(M),N,Q), ackermann(M,Q,P).

mcd(suc(X),cero,suc(X)) :- nat(X).
mcd(X,Y,Z) :- modulo(X,Y,W), mcd(Y,W,Z).


Regresar al indice

PROBLEMA DE LAS 8 REINAS

El problema de las ocho reinas consta de colocar ocho reinas en un tablero de ajedrez (una cuadricula de 8x8) de tal forma que ninguna reina este en posición de comer a otra reina. Una reina puede comer a cualquier otra reina que esta en la misma fila, columna o diagonal.
El planteamiento de fuerza bruta comprueba algunas disposiciones que podemos destacar inmediatamente.

Solución: sabemos que dos reinas no pueden aparecer en la misma fila. De este modo una solución siempre puede representarse utilizando un vector P[1...8], donde P[i] es la columna en la que esta situada la reina de la fila i-esima y por tanto las posiciones reales de las reinas vienen dadas por (1,P[1]),..(8,P[8]).

Decimos que el vector P es k-factible si ninguna de las reinas de las posiciones (1,P[1]),(2,P[2],..(K,P[k])) puede comer a otra reina de esas posiciones.

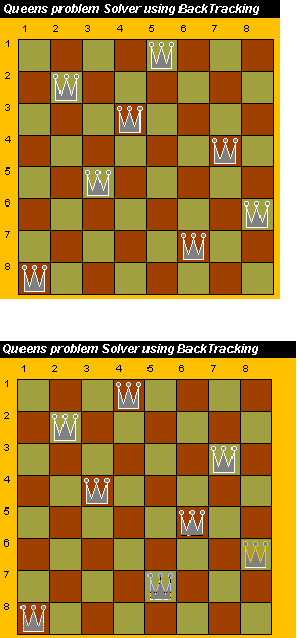
A continuación se muestra una solución a este problema generalizado a N reinas en Prolog.



/* PROBLEMA DE LAS N-REINAS */

reinas(N,Rs) :- rango(1,N,Ns), permuta(Ns,Rs), asalvo(Rs).

asalvo([R|Rs]) :- asalvo(Rs), not ataca(R,Rs).
asalvo([]).

ataca(R,Rs) :- ataca(R,1,Rs).

ataca(X,N,[Y|Ys]) :- X is Y+N; X is Y-N.
ataca(X,N,[Y|Ys]) :- N1 is N+1, ataca(X,N1,Ys).

permuta(Xs,[Z|Zs]) :- borra_primer(Z,Xs,Ys), permuta(Ys,Zs).
permuta([],[]).

borra_primer(X,[X|Xs],Xs).
borra_primer(X,[Y|Ys],[Y|Zs]) :- borra_primer(X,Ys,Zs).

rango(N,N,[N]).
rango(N,M,[N|Xs]) :- N<M, N1 is N+1, rango(N1,M,Xs).

Regresar al indice